

What are the symbolic operations that correspond to dragging each of the dots? What is true about all the legitimate things you can do to a linear equation? Why are we taught that you must do the same thing to both sides of the equation? This means that when you drag either the GREEN dot or the BLUE dot you are changing only one side of the equation!! Why is this legitimate? ĬHALLENGE - Dragging the WHITE dot changes both functions, but dragging the GREEN dot changes only the GREEN function and dragging the BLUE dot changes only the BLUE function.

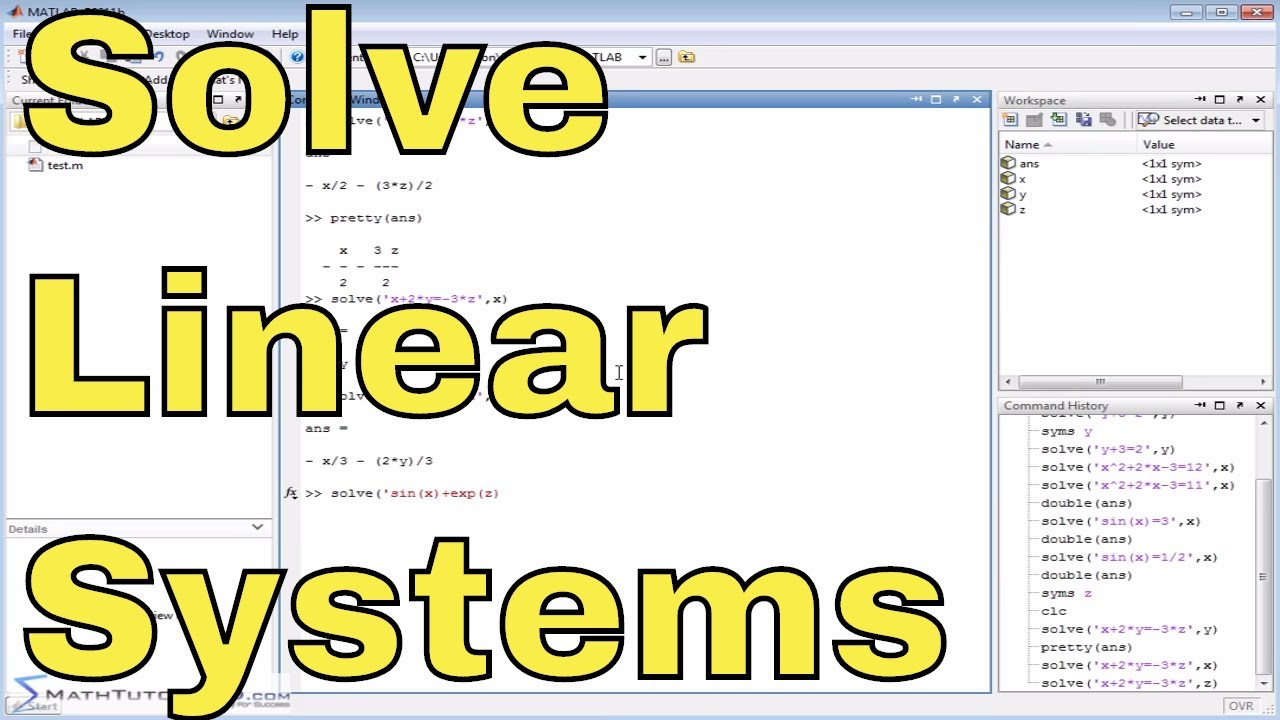
You may solve your equation graphically by dragging the GREEN, BLUE and WHITE dots on the graph in order to produce a 'solution equation' of the form x =. This applet allows you to enter a linear function f(x) = mx + b by varying m and b sliders and a function g(x) = Mx + B by varying M and B sliders. Solution of 1 Equation in 1 Unknown: octave:1> Comment: Define Function: octave:1> function y f (x) > yx3+x2-3x-3 > endfunction octave:2> Comment: Solve System for Root Starting at x0+1.0: octave:2> x, info fsolve ('f', 1.) x 1.7321 info 1 octave:3> Comment: Solve System for Root Starting at x00.0: octave:3> x, info. In this case the 'solution equation' is x = 1.5 (why is 1.5 a function?) Solving a linear equation means transforming the original equation in to a new equation that has the function x on one side of the equal sign and a number (which is a constant function) on the other side. A linear equation is always of the form f(x) = g(x).įor example, in the equation 2x - 1 = -2x + 5 we can regard f(x) as 2x - 1 and g(x) as -2x +5.


 0 kommentar(er)
0 kommentar(er)
